Cette semaine, un peu de maths ! Récemment, pour mon travail, j’ai dû faire un peu de géométrie, ça m’a pris et j’ai eu envie d’en parler ! Ça sera donc le sujet de cet article !
C’est quoi cette histoire de ressorts ?
Pour mon travail, je dois réaliser une simulation avec une plaque qui repose sur des ressorts. La particularité, c’est que ces ressorts doivent être systématiquement verticaux. Schématiquement, ça ressemble à ça :

Pour définir cet ensemble, j’ai juste besoin d’indiquer les coordonnées de chaque point (le début et la fin de la plaque, le début et la fin de chaque ressort). C’est donc ce que je fais, en écrivant dans un fichier les coordonnées de ces points. Jusque là, tout va bien !
Mais si la plaque était horizontale, ça serait trop simple. Mon problème se corse parce que la plaque peut être inclinée ! C’est-à-dire que ça peut ressembler à ceci :
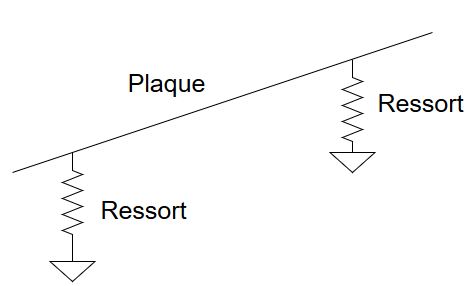
Et là, si vous observez bien, il n’y a que la plaque qui est inclinée, pas les ressorts ! C’est pour ça que je dis que ces ressorts doivent toujours être verticaux !
Comme je l’ai dit plus haut, j’ai un fichier avec les coordonnées initiales de mes points. Plutôt que d’écrire un nouveau fichier à chaque fois que je veux tester une nouvelle inclinaison, j’aimerais plutôt une astuce pour juste appliquer une rotation aux points qui doivent bouger. Et c’est ça qui m’a pas mal occupé le week-end dernier.
Formulation du problème
Pour formuler le problème, on va faire un schéma plus simple :
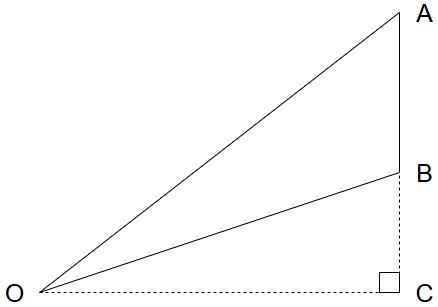
Dans ce problème, on connait plusieurs choses. Déjà, on connaît la position des points O et A. O est le début de la plaque, et A est la fin de la plaque et le début du ressort. On connait donc la distance OA, que l’on va appeler L pour notre problème.
Ensuite, on connaît l’angle AÔC, puisque c’est l’angle qu’on choisit pour incliner la plaque. On va l’appeler par la lettre grecque phi minuscule. Et enfin, le segment AB représente le ressort, on va l’appeler h. Ça, ce sont nos données.
Ensuite, on va utiliser des lettres grecques pour les angles du triangle OAB. On va appeler AÔB alpha, OÂB bêta et ABO gamma. Et il reste une dernier angle dont on a besoin, c’est l’angle CÔA, que j’appellerai epsilon.
Enfin, comme vous l’avez, remarqué, j’ai ajouté un point C qui correspond à la projection du point A sur l’axe horizontal. Et ce point-là va nous être utile très vite, vous allez voir !
Résolution
Notre question est la suivante :
Si l’on connait les valeurs de L, h et phi, quel doit être l’angle epsilon pour que AB soit égal à h ?
Pour répondre à cette question, on va commencer par s’aider de ce fameux point C ! Si vous vous souvenez de vos cours de géométrie, vous sachez sûrement que la somme des angles d’un triangle vaut 180°, ce qui correspond à pi radians. Et puisque C est la projection de A sur l’axe horizontal, on sait que l’angle ACO vaut 90°, soit pi/2 radians. Si on combine toutes ces informations, on a :
Cette égalité revient à écrire :
Ensuite, on va chercher à calculer la longueur OB, que j’appelle l. Pour cela, on va utiliser le théorème d’Al-Kashi, ou loi des cosinus. Du point de vue de l’angle beta, cela revient à écrire :
En utilisant les lois de la trigonométrie, on peut alors remplacer beta par son expression en fonction de phi, ce qui nous donne :
Ce premier résultat est déjà intéressant ! On connaît la longueur de OB en fonction de OA, AB et de l’angle phi ! Mais ce qui nous intéresse, c’est de trouver epsilon, et on n’y est pas encore !
Pour trouver epsilon, on va d’abord chercher alpha. En effet, on a l’égalité suivante :
Pour trouver alpha, on va utiliser de nouveau le théorème d’Al-Kashi, mais avec une variante ! Toujours dans OAB, on a l’égalité suivante :
Et sachant qu’on a calculé l’expression de l^2, on a alors :
Et on peut simplifier cette expression, qui devient alors :
Donc là, on a une expression de alpha qui dépend de L, h et phi, qui sont nos données ! Ça dépend aussi de l, mais on connait aussi son expression ! Donc finalement, il nous reste une dernière chose à faire, c’est exprimer epsilon en fonction de alpha, ce qui revient à :
Et voilà, on y est ! On sait donc que, pour que notre ressort reste vertical, il faut que OB = l et que l’inclinaison soit d’un angle epsilon qui dépend de nos données.
Du coup, là on est super content ! En tout cas, moi j’ai les infos qu’il me faut, donc je suis content ! Mais maintenant qu’on a cette grosse formule, on peut aussi regarder ce que ça donne comme résultats !
C’est parti pour les couleurs !
Une fois que j’ai obtenu ce résultat, je l’ai utilisé pour mon travail, mais j’ai aussi cherché à voir ce que ça pouvait donner pour différentes valeurs de phi. Et puis, comme on le voit dans l’expression, ça dépend de L, donc je voulais aussi voir son impact. Et pour ça, j’ai tracé cette figure :
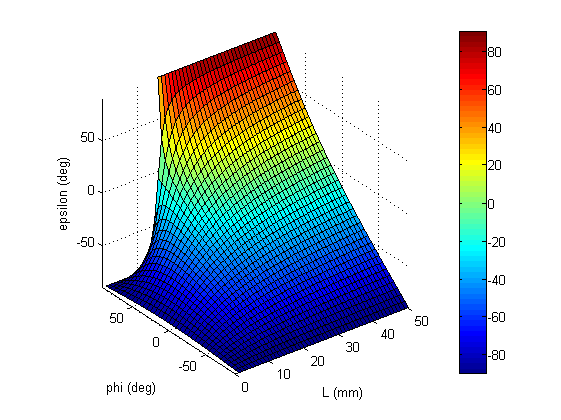
Tout de suite, c’est beaucoup plus visuel que l’équation que j’ai mise tout à l’heure ! On voit que pour des petites valeurs de L, epsilon varie assez peu et reste dans des valeurs négatives. Mais plus L augmente, plus on voit que, pour des grandes valeurs de phi, on obtient des grandes valeurs d’epsilon ! Et quand L est très grand, on voit qu’epsilon et phi sont presque égaux.
Mais il y a aussi un cas particulier, qu’on en voit pas très bien sur cette figure. Pour ça, il faut changer la vue et regarder de haut :
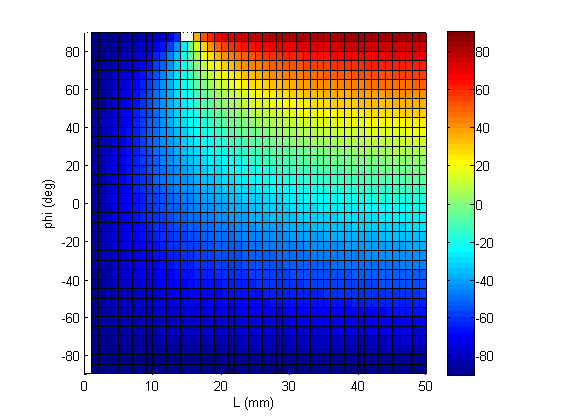
Vous avez remarqué ? Il manque un point ! Et vu qu’il manque ce point, il y a deux cases qui n’existent pas. Quel est ce point ? Eh bien c’est le point pour lequel L vaut 15mm et phi 90°. C’est un cas très particulier. Pourquoi ce point n’est pas calculé ?
Si on reprend le schéma du début avec ces deux paramètres, on observe que B, C et O sont confondus ! C’est à dire que les notions de l et de epsilon elles-mêmes n’ont plus de sens. Et ça se traduit par une impossibilité de les calculer, et donc ce fameux trou dans la courbe.
Conclusion
Voilà donc pour cette petite virée dans le monde de la géométrie ! J’espère que je ne vous ai pas trop perdu et que cet exemple vous a intéressé ! De mon côté, je trouve la figure finale très jolie ! Et il y aurait encore plein d’autres observations à faire ! Mais pour aujourd’hui, ça sera tout !
À la semaine prochaine !
Laisser un commentaire